Device Orientation Quaternion Vector Algorithm
This article describes the algorithm that is used by the Windows Hardware Certification Kit (Windows HCK) to determine the delta between the received and expected vector for 9-Axis data accuracy in the advanced orientation sensor tests. The tests validate that sensor fusion is properly integrated and that all sensors that are required for sensor fusion are properly integrated and installed.
 Note Note |
|---|
| In some cases, you can use the Sensor Diagnostic Tool to examine the 3D inclinometer and aggregated device orientation sensor that is under test. |
Quaternion vector algorithm
The algorithm uses the arc cos of the 4 dimensonal dot product of the two vectors, divided by the product of the magnitude of the two vectors and divided by 2. This algorithm is shown in Figure 1 Quaternion Vector Algorithm Formula:
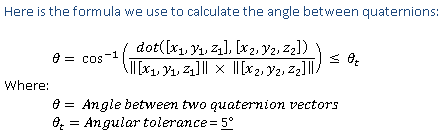
Rotation matrix values are converted to quaternion values for accuracy validation. The calculated quaternion vector should deviate no more than +/- 5 degrees from expected quaternion vector (tolerance compared against angle formed between quaternion vectors) (**+/- 10 degrees accuracy allowed on heading axis direction). The Windows HCK test allows for the Øt delta to be up to 15 degrees.
How to compute the delta angle between the received and expected Quaternion vectors
This section describes the calculation that computes the delta angle between the received and expected Quaternion vectors in Advanced Orientation Tests in the Windows HCK.
The following two data values are of interest in the data report of Aggregated Device Orientation Sensor:
-
Quaternion vector
-
Rotation matrix
The test consists of the following two verifications:
-
Verification of received Quaternion vector in the sensor data report. A Quaternion vector is of the form (xi + yj + zk + w).
-
The value of w is always expected to be positive.
-
The Quaternion vector is expected to be normalized and non-zero. For example, the magnitude of the vector must be close to 1.0. One percent (1%) leeway is provided to round off errors in the calculation of the magnitude.
-
The delta angle is calculated by using delta = 2 * Acos( ( Exp . Rec ) / ( | Exp | * | Rec | ) ), where:
* indicates scalar multiplication
. indicates dot product
Exp is the expected Quternion vector
Rec is the received Quaternion vector
| Q |indicates the magnitude of the quternion vector
delta is the angle in degrees -
If delta is greater than 360 degrees, delta is re-calculated as delta = delta – 360.
-
At this point, delta should be less than or equal to the error tolerance; for example, 10 degrees.
-
The value of w is always expected to be positive.
-
Verification of the received rotation matrix. The rotation matrix is expected to be a 3x3 matrix.
-
Each column and row vector of the rotation matrix must be normalized and non-zero. A one percent (1) leeway of is provided to round off errors in the calculation of the magnitude.
-
The received rotation matrix is transformed into a Quaternion vector.
-
All the steps from <a> to <e> of Verification (1) are re-used.
-
Each column and row vector of the rotation matrix must be normalized and non-zero. A one percent (1) leeway of is provided to round off errors in the calculation of the magnitude.
See Also
